Bài 4: Brownian Motion: Khi phấn hoa gặp gỡ giá cổ phiếu

Trong bài viết trước, chúng ta đã cùng nhau khám phá Random Walk – một mô hình thú vị nơi giá cổ phiếu nhảy múa theo từng nhịp tung đồng xu. Tuy nhiên, bạn sẽ nhận thấy một vấn đề: Biểu đồ mô phỏng trông rất thô và rời rạc. Thực tế thị trường không đứng yên chờ chúng ta tung đồng xu mỗi ngày; giá tài sản biến động liên tục trong từng mili giây.

Vậy điều gì sẽ xảy ra nếu chúng ta chia nhỏ khoảng thời gian giữa các lần tung đồng xu ra vô hạn? Khi đó, những bước nhảy rời rạc sẽ hội tụ thành một dòng chảy liên tục nhưng vẫn giữ trọn bản chất ngẫu nhiên không thể dự báo.

Chào mừng bạn đến với thế giới của Brownian Motion – nền tảng vĩ đại mà Louis Bachelier đã đặt viên gạch đầu tiên từ năm 1900 để mô tả sự biến động của giá tài sản.

Trong bài viết này:

• 1. Brownian Motion: Khi phấn hoa gặp gỡ giá cổ phiếu
  • 1.1. Lịch sử và sự tiến hóa của mô hình
    • 1.1.1. Brownian Motion – Bachelier (1900)
    • 1.1.2. Geometric Brownian Motion – Samuelson (1965)
  • 1.2. Tại sao GBM là tiêu chuẩn vàng?
  • 1.3. Giải mã GBM: Khi giải tích truyền thống bó tay trước SDE
  • 1.4. Hạn chế: Vết nứt trên viên gạch nền tảng
• 2. Thực hành mô phỏng Bachelier/GBM
  • Ví dụ
  • Thực hành Python
  • Thực hành Excel/VBA
• 3. Tóm tắt và thảo luận

1. Brownian Motion: Khi phấn hoa gặp gỡ giá cổ phiếu

Năm 1827, nhà thực vật học Robert Brown quan sát thấy các hạt phấn hoa lơ lửng trong nước di chuyển một cách hỗn loạn. Sau này, Albert Einstein chỉ ra rằng: Sự ngẫu nhiên này thực chất có thể giải thích bằng những va chạm xác định của vô số phân tử siêu nhỏ. Cùng thời điểm đó, Louis Bachelier là người đầu tiên nhận ra giá cổ phiếu cũng nhảy múa y như những hạt phấn hoa đó.

1.1. Lịch sử và sự tiến hóa của mô hình

Bachelier nhận thấy rằng nếu coi mỗi bước nhảy $X_i$ là một thông tin mới tràn vào thị trường, thì giá cổ phiếu chính là sự tích lũy của những luồng thông tin đó. Để khớp với thị trường tài chính nơi giá thay đổi liên tục từng giây, từng mili giây với các giá trị cực nhỏ, chúng ta cần chuyển dịch từ mô hình rời rạc (discrete) sang liên tục (continuous).

Thao tác nén thời gian và không gian

Các nhà toán học dùng một thao tác gọi là Donsker’s Invariance Principle. Định lý này phát biểu rằng nếu chúng ta chuẩn hóa một Random Walk bằng cách chia cho $\sqrt{n}$ (để giữ cho phương sai không bùng nổ), thì toàn bộ quỹ đạo của nó sẽ hội tụ về một Wiener Process, hay còn gọi là một Brownian Motion [1].

Cho một khoảng thời gian $t$ với $n$ bước nhảy, chúng ta phải thu nhỏ kích thước mỗi bước nhảy tương ứng với tốc độ thời gian:

• Thời gian: Mỗi bước nhảy xảy ra trong khoảng $\Delta t = \frac{t}{n}$.
• Không gian: Mỗi bước nhảy có độ lớn là $\pm \sqrt{\Delta t}$ (thay vì $\pm 1$).

Tại sao lại là căn bậc hai $\sqrt{\Delta t}$? Bởi vì theo tính chất chúng ta vừa học ở Bài 3. Random Walk, phương sai tỉ lệ thuận với số bước. Nếu mỗi bước có độ lớn $\sqrt{\Delta t}$, thì phương sai sau $n$ bước sẽ là:

Đây là một kết quả tuyệt đẹp: Phương sai của chuyển động bằng đúng khoảng thời gian trôi qua.

Sự ra đời của Wiener Process ($W_t$)

Khi $n \to \infty$, quỹ đạo thô và rời rạc của Random Walk hội tụ về một thực thể toán học hoàn hảo gọi là Wiener Process (đặt tên theo nhà toán học Norbert Wiener), ký hiệu là $W_t$.

$W_t$ thực chất là tổng tích lũy của tất cả những cú sốc ngẫu nhiên $dW_t$ từ quá khứ đến hiện tại. Trong tài chính, nó đóng vai trò là nguồn gốc của mọi sự bất định (source of randomness). Wiener Process được định nghĩa là một quy trình Markov đặc biệt có giá trị khởi đầu bằng 0, các số gia độc lập, tuân theo phân phối chuẩn với kỳ vọng bằng 0 và phương sai bằng chính khoảng thời gian trôi qua [3].

• $W_0 = 0$: Bắt đầu tại điểm gốc.
• Tính liên tục (Continuity): Quỹ đạo không bao giờ bị đứt quãng.
• Số gia độc lập (Independent Increments): Biến động tương lai không phụ thuộc vào quá khứ.
• Phân phối chuẩn (Normal Distribution): Số gia $W_t – W_s$ tuân theo phân phối chuẩn với kỳ vọng bằng 0 và phương sai bằng khoảng thời gian trôi qua ($t-s$).

Một quỹ đạo của Wiener Process điển hình liên tục ở mọi nơi nhưng không thể lấy đạo hàm tại bất kỳ điểm nào. Đồ thị của nó cực kỳ răng cưa, bao gồm toàn những góc nhọn, khiến việc vẽ chính xác bằng tay là điều không thể.

Ví dụ: Giả sử bạn muốn quan sát một Wiener Process trong vòng 1 năm với 4 bước thời gian. Thời gian mỗi bước $dt = 0.25$; độ lệch chuẩn mỗi bước $\sqrt{0.25} = 0.5$; cú sốc ngẫu nhiên $dW_t = \text{Số ngẫu nhiên} \times 0.5$. Dùng máy tính tạo số ngẫu nhiên theo phân phối chuẩn $N(0,1)$, bạn nhận được kết quả sau: $+1.2, -0.8, +0.4, -1.5$.

Quỹ đạo của Wiener Process ($Wt$) được thể hiện trong bảng dưới đây.

Vị trí $W_{0.25}, W_{0.50}, W_{0.75}, W_{1}$ phụ thuộc vào tất cả các cú sốc trước đó. Đây là lý do tại sao $W_t$ có đường đi liên tục chứ không nhảy cóc hỗn loạn giữa các giá trị không liên quan.

1.1.1. Brownian Motion – Bachelier (1900)

Tương tự như một hạt phấn hoa di chuyển trong nước do bị va chạm bởi vô số phân tử nước siêu nhỏ, Bachelier trong luận án Théorie de la spéculation đã quan niệm giá cổ phiếu là kết quả tổng hợp của vô số quyết định mua và bán độc lập, không thể dự đoán trước từ các nhà đầu tư [2].

Hãy tưởng tượng $dt$ như một nhịp đập (tick) cực nhỏ của thị trường. Tại mỗi nhịp đập này, một cú sốc ngẫu nhiên $dW_t$ được sinh ra từ luồng thông tin mới được cộng dồn vào mức giá ngay trước đó $S_{t+dt} = S_t + \sigma dW_t$.

Louis Bachelier giả định rằng giá cổ phiếu tại $t$ chính là sự tích lũy của một chuỗi những cú sốc ngẫu nhiên $dW_t$ cộng dồn từ thời điểm ban đầu.

Phương trình vi phân ngẫu nhiên (SDE) của ông có dạng:

Trong đó:

• $\sigma$: Độ biến động (Volatility) – đại diện cho sự hỗn loạn của thị trường.
• $dS_t$: Vi phân của giá – sự thay đổi giá trong khoảng thời gian cực ngắn $dt$.
• $dW_t$: Vi phân của Wiener Process – cú sốc ngẫu nhiên trong khoảng thời gian cực ngắn $dt$.

Khi nhắc tới mô hình Bachelier, mọi người hay ngầm hiểu là mô hình Bachelier đã thêm drift – mô hình Arithmetic Brownian Motion. Phương trình vi phân ngẫu nhiên của mô hình ABM này có dạng:

1.1.2. Geometric Brownian Motion – Samuelson (1965)

Công trình của Bachelier từng bị lãng quên trong nhiều thập kỷ cho đến khi nhà kinh tế học Paul Samuelson (người sau này đoạt giải Nobel) tìm thấy trong thư viện Đại học Harvard vào giữa những năm 1960 [3]. Samuelson nhận thấy tiềm năng to lớn của nó nhưng cũng thấy rõ những sai sót thực tế.

Trong mô hình gốc của Bachelier, lợi nhuận kỳ vọng bằng $0$ ($E[dS_t] = 0$). Điều này rất vô lý trong kinh tế học: Nếu bạn đầu tư vào một tài sản rủi ro (risky asset) mà không có kỳ vọng tăng trưởng, bạn thà gửi tiền vào ngân hàng cho an toàn. Samuelson đã thêm tham số $\mu$ vào mô hình để đại diện cho lợi nhuận kỳ vọng (expected return) của nhà đầu tư. Ông cũng tinh chỉnh để mô hình thực tế hơn, sự ngẫu nhiên không nên được áp dụng vào giá cổ phiếu ($S$), mà nên áp dụng vào tỷ suất sinh lời của cổ phiếu ($dS/S$).

Sau này, mô hình của Samuelson chính là nền tảng quan trọng nhất mà Black, Scholes và Merton đã sử dụng để phát triển công thức định giá quyền chọn lẫy lừng vào năm 1973 [2].

Phương trình vi phân ngẫu nhiên (SDE) cho Geometric Brownian Motion (GBM) có dạng:

Trong đó:

• $S_t$: Giá cổ phiếu tại thời điểm $t$.
• $\sigma$: Độ biến động (Volatility) – đại diện cho sự hỗn loạn của thị trường.
• $\mu$: Lợi tức dự kiến (Expected Return).
• $dS_t$: Vi phân của giá – sự thay đổi giá trong khoảng thời gian cực ngắn $dt$.
• $dW_t$: Vi phân của Wiener Process – cú sốc ngẫu nhiên trong khoảng thời gian cực ngắn $dt$.

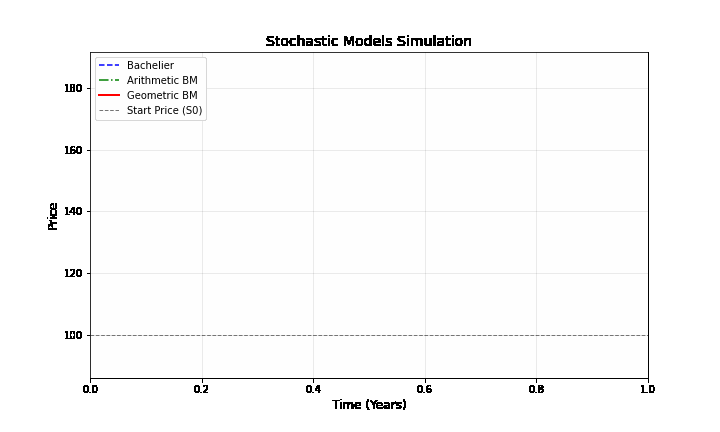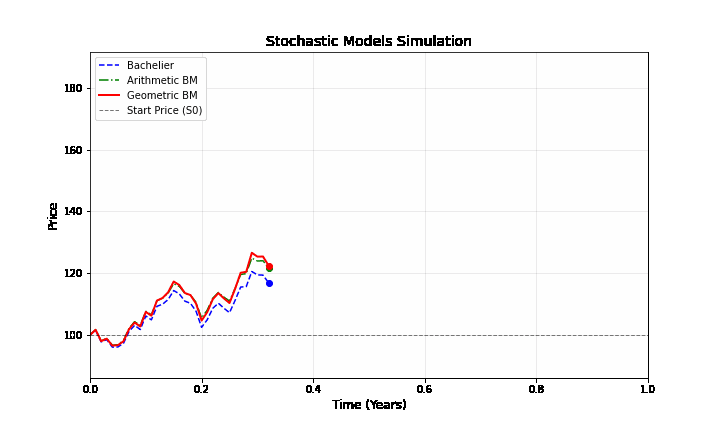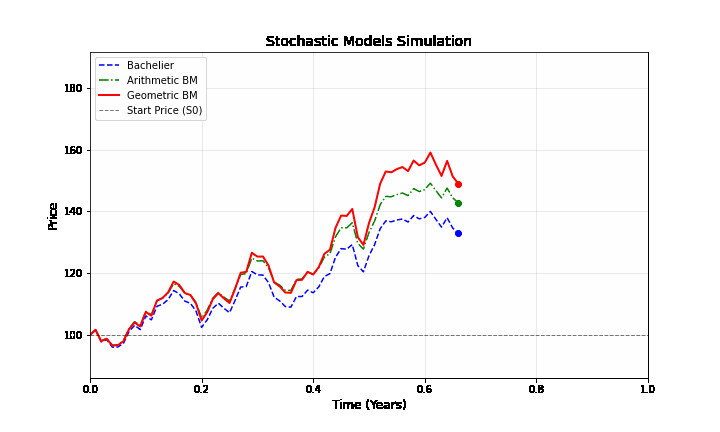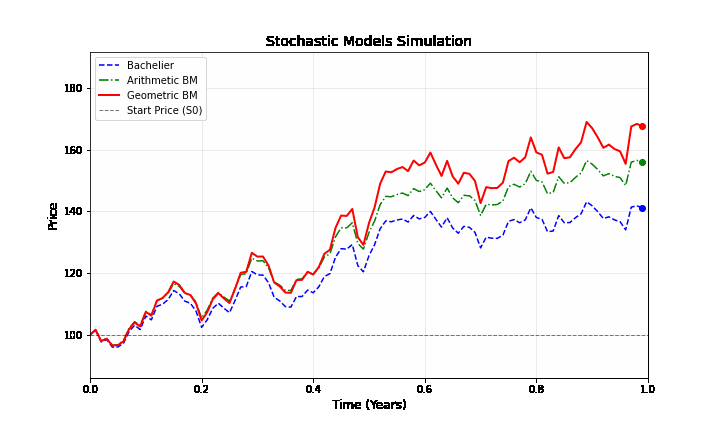
Bachelier là mô hình nguyên thủy nhất với giá chỉ dao động quanh vị trí ban đầu dựa trên các cú sốc ngẫu nhiên. Arithmetic Brownian Motion giống hệt Bachelier nhưng được cộng thêm một “lực đẩy” tuyến tính $\mu t$. Nó song song với đường Bachelier nhưng dốc lên trên theo thời gian.

Geometric Brownian Motion (GBM) là mô hình hiện đại đưa chúng ta bước vào thế giới Black-Scholes. Sự khác biệt lớn nhất là khi giá tăng, các biến động cũng khuếch đại theo. Đường màu đỏ thường có xu hướng bứt phá mạnh hơn ở vùng giá cao nhờ hiệu ứng lãi kép.

1.2. Tại sao GBM là tiêu chuẩn vàng?

Mô hình GBM cho chúng ta thấy: Giá cổ phiếu là một cuộc giằng co giữa trật tự và hỗn loạn.

• Drift ($\mu S_t dt$): Đây là phần xác định (deterministic), phản ánh giá trị nội tại và sự tăng trưởng theo thời gian. Nếu không có rủi ro ($\sigma = 0$), giá cổ phiếu sẽ tăng trưởng đều đặn như lãi suất kép với tỷ lệ $\mu$. Nó đóng vai trò như lực hấp dẫn, kéo giá cổ phiếu đi theo một xu hướng dài hạn. Nếu không có drift cao sẽ không ai chấp nhận mạo hiểm để giữ cổ phiếu.

• Volatility ($\sigma S_t dW_t$): Đây là phần ngẫu nhiên (stochastic), phản ánh tâm lý đám đông và tin tức bất ngờ. Trong đó, $\sigma$ đóng vai trò là biên độ của sự rung lắc. Nếu $\sigma$ thấp, cổ phiếu di chuyển mượt mà (như trái phiếu chính phủ). Nếu $\sigma$ cao, cổ phiếu nhảy múa điên cuồng (như Crypto). Trong ngắn hạn, phần ngẫu nhiên thường áp đảo phần xác định. Nhưng trong dài hạn, phần drift sẽ tích lũy lại và tạo ra xu hướng đi lên rõ rệt của thị trường chứng khoán [3].

Tại sao mô hình GBM lại thắng thế so với Bachelier?

• Tính không âm: Cổ đông của một công ty không thể mất nhiều hơn số tiền họ đã đầu tư. Bachelier cho phép giá âm, nghĩa là nhà đầu tư có thể phải trả thêm tiền cho việc sở hữu cổ phiếu – một điều phi lý trong kinh tế. GBM giải quyết điều này bằng cách giả định rằng logarit của giá mới tuân theo phân phối chuẩn, đảm bảo giá luôn dương.

• Phù hợp với trực giác: Nhà đầu tư thường nói “Cổ phiếu tăng 5%” chứ ít khi nói “Cổ phiếu tăng 5 USD” mà không quan tâm giá gốc là bao nhiêu.

• Lợi nhuận chuẩn: GBM phù hợp với quan sát thực tế rằng tỷ suất lợi nhuận (%) của cổ phiếu thường tuân theo phân phối chuẩn.

1.3. Giải mã GBM: Khi giải tích truyền thống bó tay trước SDE

Muốn tìm phân phối xác suất của giá cổ phiếu $S_t$, ta cần biết công thức tính giá $S_t$. Từ phương trình vi phân ngẫu nhiên (4.4) của mô hình GBM:

Chia cả hai vế cho $S_t$, rồi lấy tích phân hai vế từ thời điểm $0$ đến $t$:

Quá dễ? Có thể tích phân $\int_{0}^{t} dW_u$ hơi lạ một chút vì chứa $dW_u$, nhưng theo trực giác toán học thông thường, bạn nghĩ $\int_{0}^{t} dW_u \stackrel{?}{=} W_t \quad \text{(ĐÚNG!)}$. Bạn hoàn toàn đúng. Còn hai tích phân còn lại, với kiến thức lớp 12, bạn biết ngay $\int dx = x$ và $\int \frac{1}{x} dx = \ln(x)$. Bạn sẽ mong đợi kết quả là:

Theo giải tích ngẫu nhiên (Stochastic Calculus), kết quả cho tích phân thứ hai phải là:

Tại sao kết quả trên lại SAI? Sự khác biệt nằm ở định nghĩa của vi phân $dS_t$.

Trong giải tích cổ điển (Calculus), $dS_t$ là một sự thay đổi rất nhỏ và mịn. Nếu bạn phóng to một đường cong đủ lớn, nó sẽ trở thành một đường thẳng.

Nhưng trong thế giới ngẫu nhiên, $dS_t$ chứa $dW_t$ – số gia của Wiener Process, một thực thể với quỹ đạo cực kỳ răng cưa và biến thiên khủng khiếp. Nếu bạn phóng to nó bao nhiêu đi chăng nữa, nó vẫn răng cưa. Về mặt toán học, Wiener Process liên tục tại mọi nơi (không có đoạn ngắt quãng), nhưng không có đạo hàm tại bất kỳ điểm nào (quỹ đạo thay đổi hướng vô hạn lần trong mọi khoảng thời gian). Đạo hàm theo thời gian thực tế không tồn tại vì nó luôn tiến tới vô hạn.

Đây là nơi chúng ta thấy sự sụp đổ của giải tích Newton/Leibniz khi đối mặt với sự ngẫu nhiên. Cũng giống như việc bạn không thể dùng định luật Newton để giải thích cách một hạt ánh sáng di chuyển gần hố đen, bạn cần một lý thuyết mới – giải tích ngẫu nhiên (Stochastic Calculus) hay giải tích Itô (Itô Calculus) – để làm điều này.

Hãy coi giải tích ngẫu nhiên giống như Thuyết tương đối của Einstein trong toán học: Chúng ta không cần phải chứng minh lại toàn bộ để hiểu rằng năng lượng (energy) có thể biến đổi thành khối lượng (mass). Bạn hãy tạm chấp nhận lời giải từ các nhà toán học và dùng kết quả đó để hiểu giá cổ phiếu tuân theo phân phối gì.

Mô hình Bachelier, giải phương trình (4.3) ta có công thức tính giá như sau:

Chuyển vế $S_0$, ta có:

Theo tính chất (4.1) với $s = 0$, ta có $W_t \sim N(0, t)$. Vì $W_t$ tuân theo phân phối chuẩn, nên khi thực hiện phép cộng theo công thức (4.5), kết quả $S_t$ cũng tuân theo phân phối chuẩn.

Lập luận tương tự cho phương trình (4.6), số hạng vế trái $S_t - S_0$, mô tả cho lợi nhuận tuyệt đối (absolute return), cũng tuân theo phân phối chuẩn.

Mô hình GBM, giải phương trình (4.4) ta có công thức tính giá như sau:

Lấy logarit tự nhiên ($\ln$) hai vế của phương trình (4.7), ta có:

Vế phải của phương trình (4.8) và (4.9) có cấu trúc tương đồng với phương trình (4.5): Đó là phép cộng biến ngẫu nhiên $W_t$. Tương tự như trên, ta có $\ln(S_t)$ và $\ln\left(\frac{S_t}{S_0}\right)$ (log return) tuân theo phân phối chuẩn. Điều này tương đương với $S_t$ tuân theo phân phối log-chuẩn.

Trong Random Walk chúng ta dùng $n$ (số bước), nhưng khi sang Bachelier và GBM chúng ta dùng $t$ (thời gian). Đây chính là sự chuyển dịch từ rời rạc sang liên tục. Phương sai $\sigma^2$ trong các mô hình liên tục thực chất là sự mịn hóa của phương sai $4pq$ trong mô hình rời rạc.

Điểm thú vị nhất là sự xuất hiện của $-\frac{\sigma^2}{2}$ trong mô hình GBM. Đây là điểm khác biệt lớn nhất về mặt toán học giữa mô hình cộng và mô hình nhân, giải thích tại sao biến động mạnh có thể làm xói mòn lợi nhuận thực tế.

1.4. Hạn chế: Vết nứt trên viên gạch nền tảng

Dù Bachelier và GBM là viên gạch nền móng cho tài chính hiện đại, chúng ta cần thẳng thắn thừa nhận rằng mô hình này dựa trên những giả định lý tưởng hóa mà thực tế thị trường thường xuyên vi phạm:

• Giả định phân phối chuẩn: Bachelier giả định absolute return, GBM giả định log return tuân theo phân phối chuẩn. Tuy nhiên, dữ liệu thực tế thường cho thấy thị trường có hiện tượng “đuôi béo” (fat tails). Nghĩa là, các biến cố cực đoan, như thị trường sụp đổ hoặc tăng trưởng nóng, xảy ra với tần suất cao hơn nhiều so với dự báo của mô hình.

• Giả định độ biến động là hằng số (constant volatility): Chúng ta giả định độ biến động ($\sigma$) trong phương trình (4.3) và (4.4) là một hằng số cố định. Thực tế, biến động của thị trường có tính “co cụm” (volatility clustering) – những giai đoạn biến động mạnh thường đi cùng nhau và ngược lại.

• Giả định bước nhảy độc lập: Mô hình giả định các bước nhảy là độc lập (Markov Property), nhưng đôi khi thị trường có “trí nhớ”, nơi các xu hướng trong quá khứ có thể ảnh hưởng đến tâm lý đám đông trong tương lai.

Đừng coi các mô hình tài chính như những định luật vật lý bất biến. Hãy coi chúng như một hầm gió (wind tunnel). Trong hầm gió, chúng ta tạo ra một môi trường lý tưởng hóa để thử nghiệm các cấu trúc tài chính trước khi đưa chúng ra đối mặt với bầu trời thực đầy giông bão của thị trường. Một mô hình tốt không nhất thiết phải là một bản mô tả hoàn hảo về thực tại, mà là một công cụ giúp chúng ta hiểu rõ các biến số đầu vào ảnh hưởng thế nào đến giá trị [4].

Bachelier và GBM chính là kiểu mô hình như vậy, đặc biệt hữu ích cho người mới bắt đầu. Mô hình đơn giản giúp ta hiểu bản chất, có công thức đóng (closed-formula) giúp việc thực thi trở nên đơn giản, và là một hệ quy chiếu chuẩn mực (benchmark) cho các mô hình phức tạp hơn.

2. Thực hành mô phỏng Bachelier/GBM

Ví dụ

• Cổ phiếu X
• Giá hiện tại ($S_0$): $100$
• Lợi nhuận kỳ vọng ($\mu$): $10\%$ mỗi năm
• Độ biến động ($\sigma$): $40\%$ mỗi năm
• Thời gian ($t$): $1$ năm

Mô hình Bachelier (Arithmetic Brownian Motion)

Trong mô hình này, lợi nhuận kỳ vọng và độ biến động được tính bằng số tiền tuyệt đối:

Công thức tính giá cổ phiếu:

Kịch bản 1: Thị trường đi ngang ($W_t = 0$)

Kịch bản 2: Thị trường xấu đi ($W_t = -3$)

Mô hình Samuelson (Geometric Brownian Motion)

Chúng ta tạm mượn công thức tính giá cổ phiếu từ giải tích ngẫu nhiên:

Tốc độ tăng trưởng thực tế sau điều chỉnh $-\frac{\sigma^2}{2}$:

Kịch bản 1: Thị trường đi ngang ($W_t = 0$)

Trong khi Bachelier hứa hẹn mức giá $110$, GBM cảnh báo bạn rằng biến động quá cao ($40\%$) sẽ bào mòn lợi nhuận và giá thực tế bạn nhận được chỉ là $102$. Đây chính là volatility drag – kẻ thù thầm lặng của mọi nhà đầu tư mà chỉ có giải tích ngẫu nhiên mới chỉ ra được.

Kịch bản 2: Thị trường xấu đi ($W_t = -3$)

Trong khi Bachelier đưa ra một giá trị âm, GBM giữ cho nó sống sót ở mức $30.73$ – phản ánh đúng thực tế giá giảm sâu nhưng không bao giờ âm.

Thực hành Python

Dưới đây là source code Python mô phỏng 100 000 kịch bản cho ví dụ trên với các tham số được giữ nguyên: $S_0 = 100, \mu = 10\%, \sigma = 40\%, T = 1$ năm.

Chúng ta cần khai báo thư viện và các biến số như giả thiết của bài toán.

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1.inset_locator import inset_axes

# --- 1. Configuration ---
S0 = 100          # Initial Stock Price
mu = 0.10         # Expected Return (10%)
sigma = 0.40      # Volatility (40%)
T = 1.0           # Time Horizon (1 Year)
steps = 252       # Number of time steps (Daily)
dt = T / steps    # Time increment
n_simulations = 100000 # Increased for smoother histograms

Tiếp theo, ta tính giá cố phiếu theo Bachelier và GBM.

Hàm np.random.normal tạo ra một vector gồm 100 000 số ngẫu nhiên tuân theo quy luật phân phối chuẩn. Từ công thức (4.1) với $t = T, s = 0$ ta có $W_T \sim N(0, T)$ – kỳ vọng bằng 0 0 và độ lệch chuẩn bằng căn bậc hai của thời gian T np.sqrt(T). Ta gán 100 000 số ngẫu nhiên vào công thức (4.5) cho Bachelier và (4.7) cho GBM để tính giá cố phiếu tại vị trí cuối cùng.

# --- 2. Generate random terminal Brownian Motion values W_T ~ N(0, T) ---
W_T = np.random.normal(0, np.sqrt(T), n_simulations)
S_T_bachelier = S0 + (mu * S0) * T + (sigma * S0) * W_T
S_T_gbm = S0 * np.exp((mu - 0.5 * sigma**2) * T + sigma * W_T)

# Calculate theoretical median
median_bachelier = S0 + (mu * S0) * T 
median_gbm = S0 * np.exp((mu - 0.5 * sigma**2) * T)

Ta thử kiểm tra Wiener Process W_T. Vì $W_T \sim N(0, T)$, khoảng 95% số được tạo ra sẽ nằm trong khoảng 2 độ lệch chuẩn ($\mu \pm 2\sigma$) hay trong ví dụ này là ($\pm 2$).

print('W_T = ')
print(W_T)

W_T = 
[-0.02641451  0.56418443  0.47622705 ...  1.26794091  0.22876935
 -0.19311188]

Cuối cùng, ta vẽ biểu đồ Histogram so sánh giữa hai mô hình Bachelier và GBM.

# --- 3. Plot Histograms ---
fig, ax = plt.subplots(figsize=(10, 6))

ax.hist(S_T_bachelier, bins=200, alpha=0.4, color='red', 
        label='Bachelier (Normal Distribution)', density=True)
ax.hist(S_T_gbm, bins=200, alpha=0.4, color='blue', 
        label='GBM (Log-normal Distribution)', density=True)

# --- 4. Median Lines (The visual "centers" of the peaks) ---
ax.axvline(median_bachelier, color='darkred', linestyle='--', linewidth=2.5,
           label=f'Median Bachelier: {median_bachelier:.2f}')
ax.axvline(median_gbm, color='darkblue', linestyle='--', linewidth=2.5,
           label=f'Median GBM: {median_gbm:.2f}')

# --- 5.Formatting ---
ax.set_title("Bachelier vs. GBM: The Failure of Normal Distribution in Modelling Stock Price")
ax.set_xlabel("Final Price")
ax.set_ylabel("Probability Density")
ax.legend(loc='lower right')

plt.tight_layout()
plt.show()

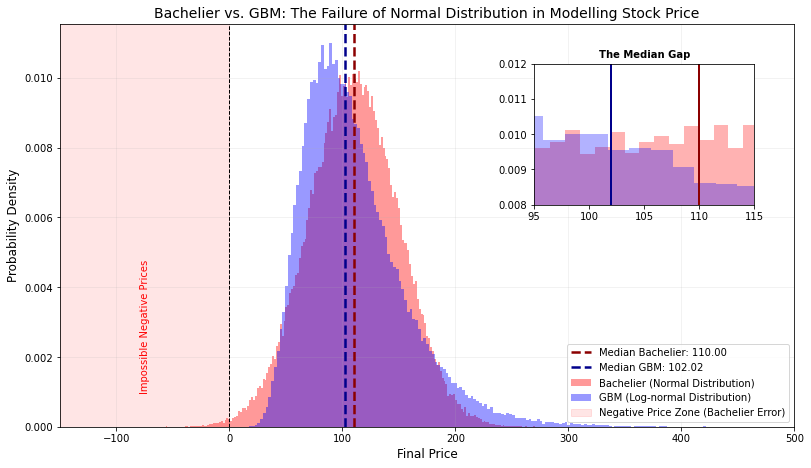
Biểu đồ này cho thấy sự khác biệt giữa hai mô hình:

• Bachelier (vàng): Là một hình chuông đối xứng hoàn hảo (Normal Distribution). Điều này hàm ý rằng xác suất cổ phiếu tăng 50 cũng bằng xác suất nó giảm 50. Với tham số đã cho có khoảng 0.3% trường hợp giá cổ phiếu sẽ kết thúc ở mức dưới 0 (vùng tô màu đỏ nhạt), điều vốn bất khả thi trong kinh tế học.

• GBM (xanh): Là một hình chuông bị lệch phải (Log-normal Distribution), với phần đuôi dài về phía giá cao nhưng bị chặn đứng tại mức 0. Điều này phản ánh đúng thực tế: Bạn chỉ có thể lỗ tối đa 100% số tiền đầu tư. Mặc dù kỳ vọng (expectation) là $110$, nhưng trung vị (median) của GBM chỉ đạt khoảng $101.6$. Sự chênh lệch này là do phần $-\frac{\sigma^2}{2}$ (volatility drag) gây ra.

Phần tiếp theo, tôi cố tình ép Wiener Process ($W_t = -3$) để mô tả kịch bản thị trường sụp đổ.

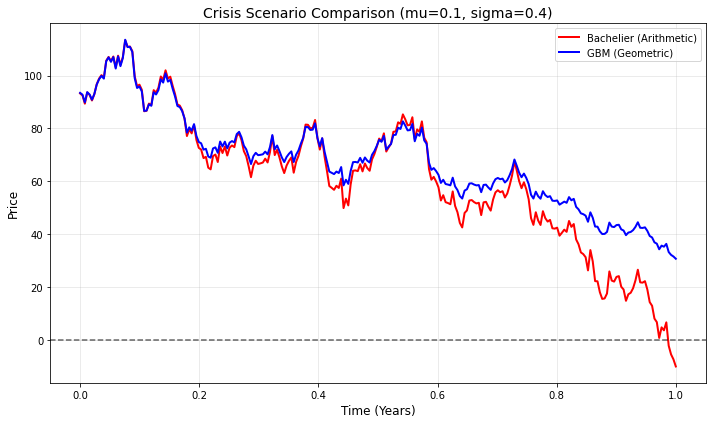
Theo kết quả tính toán lý thuyết, ta có $S_t = -10$ với Bachelier và $S_t = 30.73$ với GBM, khớp hoàn toàn với biểu đồ mô phỏng. Bạn sẽ thấy đường màu vàng Bachelier đâm xuyên qua trục 0, trong khi đường màu xanh GBM dù giảm sâu nhưng vẫn giữ được giá trị dương.

Thực hành Excel/VBA

Bạn có thể download file Excel bên dưới để bắt đầu thực hành.

Excel Workbook

Worksheet 1 “Standalone Bachelier GBM”: Trang tính này mô phỏng quỹ đạo của một cổ phiếu đơn lẻ trong vòng một năm với 252 ngày giao dịch. Bạn có thể điều chỉnh các tham số $\mu$ (drift) và $\sigma$ (volatility) để quan sát các hành vi ngẫu nhiên khác nhau.

Công thức tại ô B10 như sau.

=NORM.S.INV(RAND())

Hàm RAND() được dùng để tạo một số ngẫu nhiên bất kỳ từ 0 đến 1. Hàm NORM.S.INV() là hàm nghịch đảo của phân phối chuẩn, có nhiệm vụ biến đổi một xác suất (từ 0 đến 1) thành một giá trị $z-score$ tương ứng trên đường cong hình chuông.

$dW_t$ thực chất là $Z \sqrt{dt}$, trong đó $Z$ là một biến ngẫu nhiên có phân phối chuẩn hóa (Standard Normal Distribution) $Z \sim N(0, 1)$. Việc sử dụng NORM.S.INV(RAND()) trong Excel chính là cách chúng ta tạo ra giá trị $Z$ này cho mỗi bước thời gian.

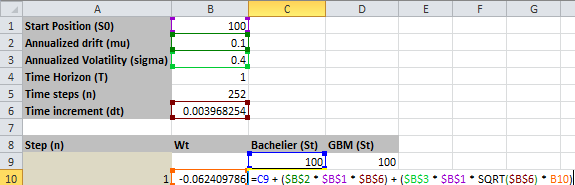
Công thức tại ô C10 như sau.

=C9 + ($B$2 * $B$1 * $B$6) + ($B$3 * $B$1 * SQRT($B$6) * B10)

Đây chính là công thức giá (4.5) trong mô hình Bachelier. Tuy nhiên cần chú ý, các tham số $\mu$ và $\sigma$ đều phải ở dạng giá trị tuyệt đối (đơn vị tiền tệ) thay vì tỷ lệ phần trăm. Ta cần nhân thêm giá cổ phiếu ban đầu $B$1 vào $\mu$ và $\sigma$.

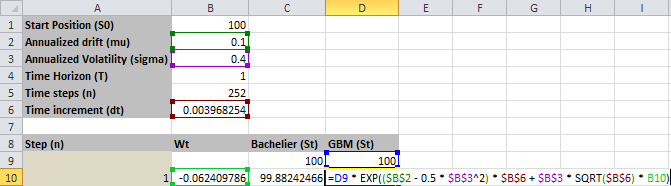
Công thức tại ô D10 như sau.

=D9 * EXP(($B$2 - 0.5 * $B$3^2) * $B$6 + $B$3 * SQRT($B$6) * B10)

Đây chính là công thức giá (4.7) trong mô hình GBM với sự xuất hiện của phần volatility drag $-\frac{\sigma^2}{2}$

Chọn ô A9:D9 rồi kéo xuống đến dòng 261 (tương ứng 252 bước). Dựa trên kết quả từ C9:C261 và D9:D261, ta vẽ được biểu đồ lộ trình cho giá cổ phiếu theo Bachelier và GBM như dưới đây.

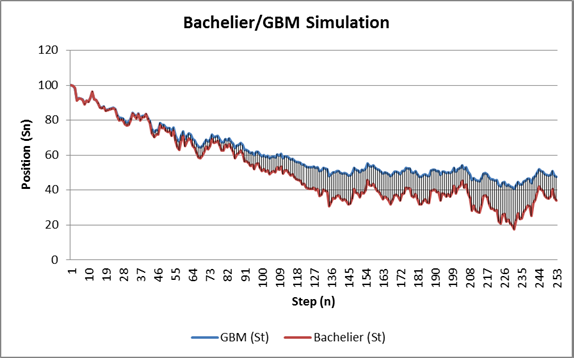
Bạn có thể nhấn phím F9 trong Excel để hàm RAND() sinh một bộ số ngẫu nhiên mới. Bạn sẽ thấy lộ trình Bachelier và GBM bám khá sát nhau, chỉ lệch ra xa trong đoạn đồ thị có xu hướng rõ rệt (tăng liên tiếp hoặc giảm liên tiếp).

Worksheet 2 “Distribution Analysis”: Trang tính này minh họa phân phối xác suất thực nghiệm của giá cổ phiếu trong hai mô hình Bachelier và GBM.

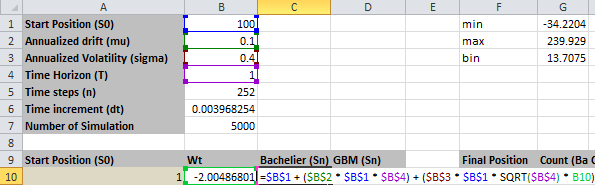
Công thức tại ô C10 và D10 như sau.

=$B$1 + ($B$2 * $B$1 * $B$4) + ($B$3 * $B$1 * SQRT($B$4) * B10)

=$B$1 * EXP(($B$2 - 0.5 * $B$3^2) * $B$4 + $B$3 * SQRT($B$4) * B10)

Giống hệt phần trên, ta vẫn dùng công thức (4.5) và (4.7). Khác biệt duy nhất là thay vì dùng $dt$ ta dùng $T$ để có luôn giá cổ phiếu tại vị trí cuối cùng.

Công thức tại ô G10 như sau.

=COUNTIFS($C$10:$C$5009, ">=" & F10, $C$10:$C$5009, "<" & F11)

Vì giá cổ phiếu tại vị trí kết thúc không còn là số nguyên biết trước như trong trường hợp Random Walk, để vẽ biểu đồ Histogram sẽ phức tạp hơn. Chúng ta tự tạo 20 khoảng chia (bins) bằng nhau, với giá trị từ thấp lên cao. Công thức ở ô G10 giúp ta đếm số lượng mẫu tại mỗi bins.

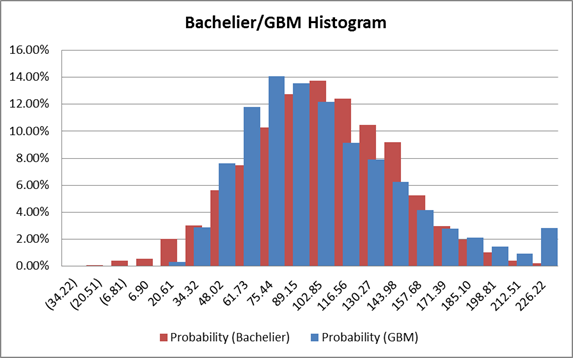
Tương tự phần Python, ta thấy rõ sự khác biệt phân phối xác suất giữa hai mô hình. Bachelier (vàng) với dạng hình chuông đối xứng hoàn hảo (Normal Distribution), trong khi đó GBM (xanh) với đỉnh bị lệch trái rõ rệt với phần đuôi dài về phía giá cao (Log-normal Distribution).

3. Tóm tắt và thảo luận

Trong bài viết này, chúng ta đã có một bước tiến về mặt toán học, cũng như một sự thay đổi tư duy trong việc nhìn nhận rủi ro tài chính.

• Sự tiến hóa của mô hình: Louis Bachelier là người đầu tiên đưa sự ngẫu nhiên vào tài chính. Tuy nhiên, sai lầm của ông (coi biến động là số tiền tuyệt đối) đã được Paul Samuelson sửa chữa bằng cách coi biến động là tỷ lệ phần trăm. Bachelier giống như cộng tiền vào ví. GBM giống như nhân tài khoản theo lãi kép, nhưng có trừ đi một khoản “thuế rủi ro” do chính sự rung động của thị trường tạo ra.

• Nhu cầu lý thuyết mới: Việc chuyển từ rời rạc (discrete) sang liên tục (continuous) khiến các phương pháp số học thông thường trở nên vô dụng. Chúng ta cần các công cụ của giải tích ngẫu nhiên (Stochastic Calculus) để giải quyết các bài toán.

• Phân phối xác suất: Trong GBM, mặc dù lợi nhuận (log return) tuân theo phân phối chuẩn, nhưng giá tài sản lại tuân theo phân phối log-chuẩn để đảm bảo giá không bao giờ âm.

• Mô phỏng mô hình: Qua việc thực hành trên Python/Excel, chúng ta thấy rằng các tham số $\mu$ (drift) và $\sigma$ (volatility) chính là linh hồn điều khiển quỹ đạo của mô phỏng.

• Thực hành Python

• Thực hành Excel Excel Workbook

Trong vật lý, một mô hình được coi là đúng nếu nó dự báo chính xác quỹ đạo của các hành tinh. Nhưng tài chính là một ngành khoa học xã hội, nơi thị trường là đấu trường của hành động (action) và phản ứng (reaction). Con người học hỏi từ những sai lầm trong quá khứ và không lặp lại chúng một cách máy móc.

Do đó, Bachelier hay GBM không nên được xem là những giáo điều thống kê, mà nên là những công cụ để đảm bảo tính nhất quán giữa các công cụ tài chính khác nhau, sao cho không có kinh doanh chênh lệch giá (no-arbitrage) [4].

Trước khi sang bài tiếp theo, hãy cùng suy ngẫm về câu hỏi dưới đây:

• Theo bạn, tham số nào quan trọng hơn khi dự báo giá: xu hướng tăng trưởng (drift) hay mức độ rung lắc (volatility)?

• Trong ngắn hạn, nhiễu (noise) thường lấn át tín hiệu (signal). Vậy theo bạn, các trader giao dịch trong ngày đang thực sự giao dịch dựa trên quy luật, hay chỉ đang ‘đánh cược’ với những rung động ngẫu nhiên của thị trường?

Hãy để lại ý kiến ở phần bình luận nhé!