Bài 3: Random Walk: Đầu tư hay tung đồng xu?
Từ "xác định" tới "ngẫu nhiên", cùng tìm hiểu về Random Walk trong tài chính.
Trong bài viết trước, sau khi theo chân Emanuel Derman bước qua những hành lang quyền lực tại Phố Wall, chúng ta nhận ra rằng cốt lõi của nghề Quant nằm ở khát vọng mô hình hóa thế giới. Nhưng làm thế nào để chúng ta mô hình hóa một thứ dường như hoàn toàn hỗn loạn như giá cổ phiếu? Liệu những dòng code và phương trình toán học có đủ quyền năng để “dự đoán” tương lai?
Hôm nay, chúng ta sẽ bắt đầu hành trình đi tìm “trật tự” trong sự “ngẫu nhiên”.
Trong trang này:
- 1. Từ “xác định” tới “ngẫu nhiên”
- 2. Random Walk: Trò chơi tung đồng xu
- 3. Tóm tắt và thảo luận
- 4. Tài liệu tham khảo
1. Từ “xác định” tới “ngẫu nhiên”
Trong suốt hàng thế kỷ, khoa học bị thống trị bởi tư duy Xác định/Định mệnh (Deterministic). Đỉnh cao của tư tưởng này là Laplace’s Demon — một giả thuyết cho rằng nếu một ai đó hay “ác quỷ” biết được vị trí và vận tốc của mọi hạt trong vũ trụ tại một thời điểm, thì giá trị quá khứ và tương lai của chúng tại bất kỳ thời điểm nào đều được suy ra.
Thế giới xác định (Deterministic)
Trong thế giới này, mọi thứ vận hành giống như một kịch bản phim đã viết sẵn. Nếu bạn biết đầu vào \(x\), bạn chắc chắn có đầu ra \(y\), thông qua công thức \(y = f(x)\).
Khi NASA phóng một tàu thăm dò lên Sao Hỏa, họ sử dụng các phương trình vi phân xác định. Dù hành trình dài hàng triệu dặm, nhưng nhờ các định luật Newton, họ biết chính xác tàu sẽ ở đâu vào giây thứ \(n\). Sai số chỉ đến từ việc đo lường, không phải từ bản chất của vũ trụ.
Trong tài chính cổ điển, người ta từng mơ mộng về việc tìm ra một công thức toán học “cứng”, hay là đi tìm một hàm \(y = f(x)\) như thế.
Khi Phố Wall không phải là Sao Hỏa
Khi các nhà khoa học mang tư duy này vào tài chính, họ sớm nhận ra một “cú sốc”. Giá cổ phiếu không vận hành theo các định luật Newton. Nó không rơi theo một đường thẳng, nó nhảy múa, rung lắc và đôi khi đảo chiều một cách không tưởng.
Bạn không thể dùng vận tốc tăng trưởng giá cổ phiếu của ngày hôm qua để khẳng định vị trí giá cổ phiếu của ngày hôm nay.
Thế giới ngẫu nhiên (Stochastic)
Stochastic không có nghĩa là “vô định” hay “hỗn loạn”. Giống như một trò chơi tung xúc xắc liên tục. Bạn không biết chính xác số tiếp theo là gì, nhưng bạn có thể biết xác suất của nó.
Để bạn đọc dễ hình dung, hãy so sánh hai cách nhìn về một khoản đầu tư:
-
Góc nhìn xác định (lãi suất tiết kiệm): Bạn gửi 1 tỷ vào ngân hàng với lãi suất 7%/năm. Bạn biết chắc chắn sau 10 năm mình có bao nhiêu tiền. Biểu đồ là một đường cong mượt mà, đi lên đều đặn, giống như một hàm số trong toán học.
-
Góc nhìn ngẫu nhiên (thị trường chứng khoán): Bạn mua 1 tỷ cổ phiếu Apple. Trung bình nó có thể tăng 10%/năm, nhưng trên đường đi, nó có thể giảm 20% vì một tin tức chính trị, hoặc tăng 15% vì một dòng tweet. Biểu đồ giá cổ phiếu là một đường răng cưa hỗn loạn.
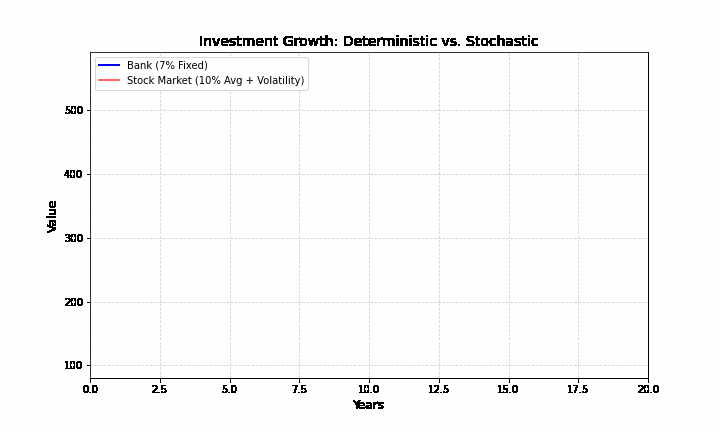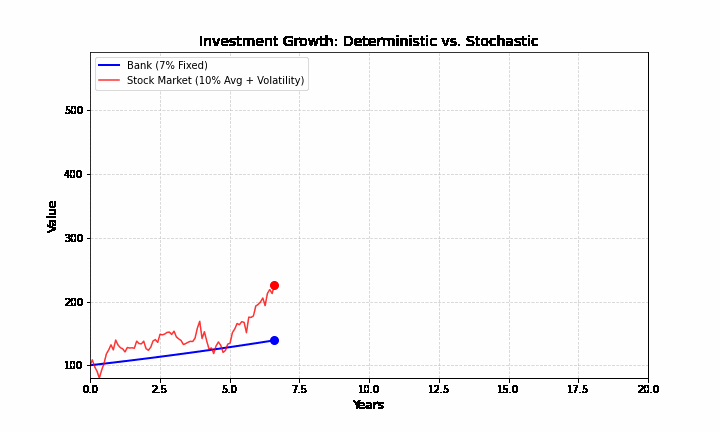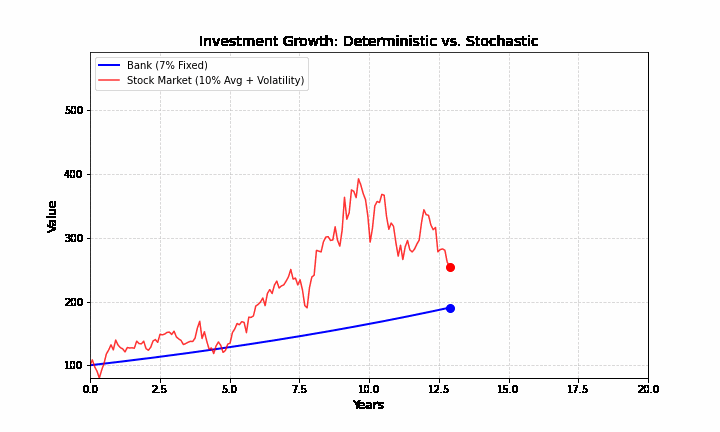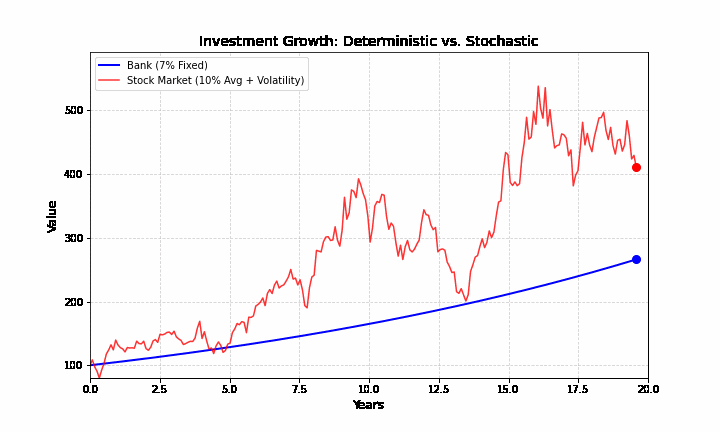
Sự giằng xé giữa hai thế giới
Sự đối lập giữa tính xác định và ngẫu nhiên có một lịch sử trí tuệ lâu đời vượt xa phạm vi tài chính.
Đầu thế kỷ 20, Albert Einstein khi nghiên cứu chuyển động hỗn loạn của các hạt phấn hoa đã chỉ ra rằng: sự ngẫu nhiên này thực chất có thể giải thích bằng những va chạm xác định của vô số phân tử siêu nhỏ. Hiện tượng này trông có vẻ ngẫu nhiên chỉ vì chúng ta không thể theo dõi hết số lượng khổng lồ các nguyên nhân tiềm ẩn bên dưới.
Thật kinh ngạc, cùng thời điểm đó vào năm 1900, Louis Bachelier đã đưa sự ngẫu nhiên vào mô hình tài chính trong luận án tiến sĩ Théorie de la spéculation. Bachelier là người tiên phong dùng Brownian Motion để mô tả sự biến động của giá tài sản, từ rất lâu trước khi nó trở thành khái niệm trung tâm của tài chính hiện đại. Sau này, các nhà kinh tế học như Paul Samuelson và Robert C. Merton đã kế thừa và phát triển chúng thành mô hình Black-Scholes-Merton lẫy lừng.
Sự sụp đổ của thế giới xác định trong tài chính đến từ nhận định: rủi ro không phải là sai số, rủi ro là bản chất. Nếu bạn lập kế hoạch tài chính dựa trên một con số “trung bình” xác định, bạn sẽ “cháy tài khoản” ngay khi thị trường rung lắc mạnh. Các Quant thành công không phải là những người dự báo đúng giá ngày mai, mà là những người mô hình hóa chính xác độ lớn của sự rung lắc đó.
Tuy nhiên, cuộc tranh luận này vẫn chưa dừng lại. Những học giả như Benoît Mandelbrot sau này đã đặt câu hỏi: “Liệu thị trường là ngẫu nhiên thực sự, hay chúng là những cấu trúc hữu định cực kỳ phức tạp mà các mô hình hiện tại của chúng ta chưa thể nắm bắt hết?”. Việc sử dụng xác suất trong tài chính thường mang tính “tiện lợi về mặt phương pháp luận” hơn là một lời khẳng định cuối cùng về bản chất thật sự của thị trường.
Bạn có suy nghĩ gì về vấn đề này? Hãy để lại ý kiến ở phần bình luận nhé!
2. Random Walk: Trò chơi tung đồng xu
Trong vật lý cổ điển, mục tiêu của chúng ta là tìm ra quỹ đạo chính xác của vật thể. Trong tài chính, các nhà toán học cũng nỗ lực làm điều tương tự: mô hình hóa quỹ đạo của giá cổ phiếu. Để làm điều này, các nhà toán học bắt đầu bằng một trò chơi đơn giản nhất: tung đồng xu.
2.1. Bài toán
Bài toán gốc: Hãy tưởng tượng bạn đang đứng tại vạch số 0 (ký hiệu là \(S_0\)) trên một trục số dài vô tận. Bạn cầm trên tay một đồng xu và bắt đầu một trò chơi.
- Mỗi khi tung được mặt Ngửa, bạn bước sang phải 1 bước \((+1)\).
- Mỗi khi tung được mặt Sấp, bạn bước sang trái 1 bước \((-1)\).
Kết quả mỗi lần tung là một biến ngẫu nhiên \(X_i\) nhận hai giá trị \(\pm 1\). Vì xác suất Ngửa/Sấp là \(50/50\) nên trò chơi này là một bước đi ngẫu nhiên đối xứng (Symmetric Random Walk).
Vị trí của bạn sau \(n\) lần (ký hiệu là \(S_n\)) chính là tổng của tất cả các bước đi từ vị trí đầu tiên:
\[S_n = S_0 + X_1 + X_2 + \dots + X_n ~~~~(1)\]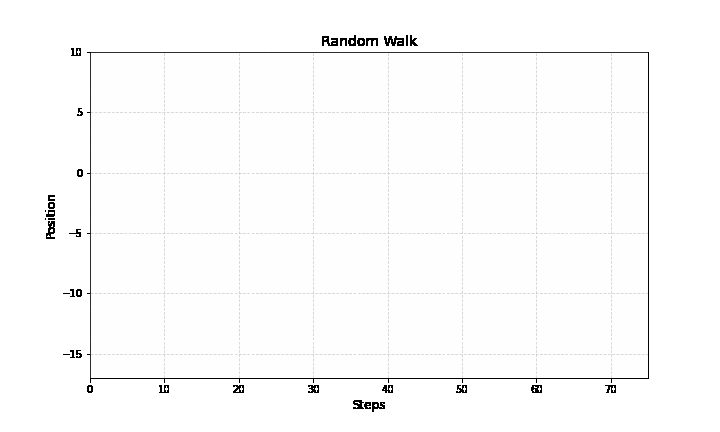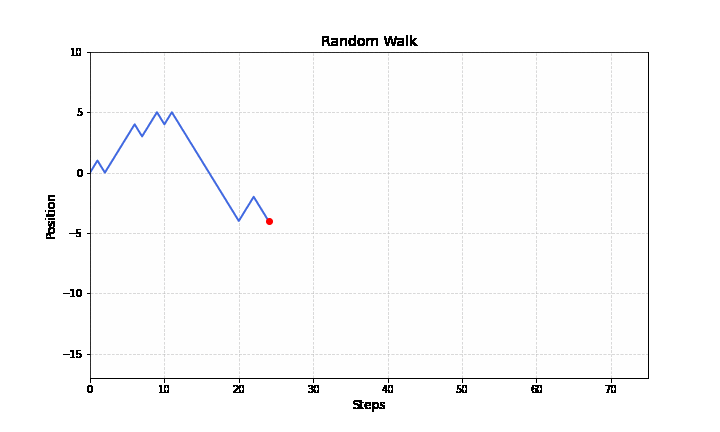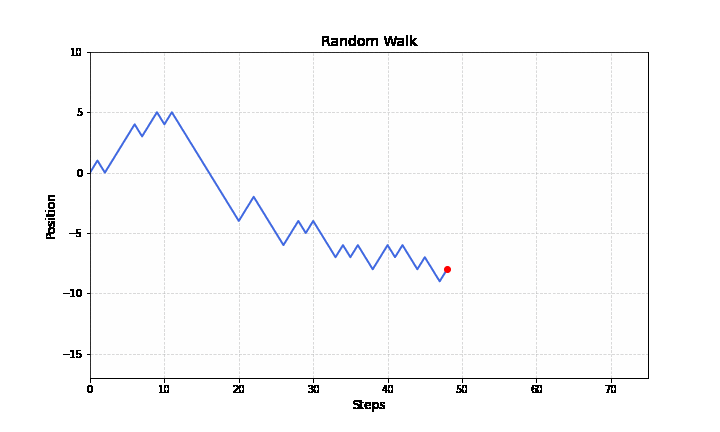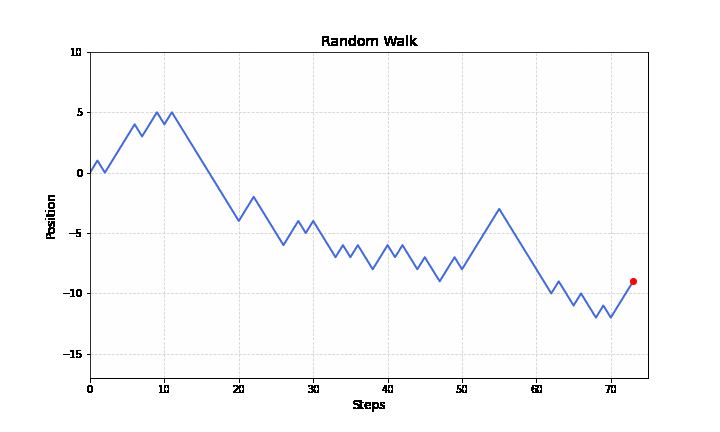
Ví dụ: Bạn chơi trò chơi này 3 lần. Bạn tung đồng xu và nhận được các giá trị lần lượt là: Ngửa, Ngửa, Sấp. Với giả thiết bài toán như trên, bạn có: Vị trí đứng ban đầu: \(S_0 = 0\); Giá trị ba lần tung đồng xu: \(X_1 = 1\), \(X_2 = 1\), \(X_3 = -1\); Vị trí cuối cùng: \(S_3 = S_0 + X_1 + X_2 + X_3 = 0 + 1 + 1 - 1 = 1\). Tức là bạn đứng lệch một bước về phía bên phải sau 3 lần chơi.
Bài toán tổng quát: Giả sử giá cổ phiếu hôm nay là \(S_0\). Trong mỗi bước thời gian \(i \in \{1, 2, \dots, n\}\), giá cổ phiếu sẽ tăng/giảm theo một biến ngẫu nhiên \(X_i\) nhận hai giá trị \(\pm 1\).
- \(n\): tổng số bước
- \(n_u\): số bước tăng
- \(n_d\): số bước giảm
- \(k\): vị trí cuối
- \(X_i = +1\) với xác suất \(p\)
- \(X_i = -1\) với xác suất \(q = 1 - p\)
Giá cổ phiếu tăng/giảm tại mỗi bước thời gian \(i\):
\[\Delta S_i = X_i ~~~~(2)\]Giá cổ phiếu sau \(n\) bước sẽ là:
\[S_n = S_0 + \sum_{i=1}^{n} X_i ~~~~(3)\]Mục tiêu của bài toán là đi tìm xác suất giá cổ phiếu ở vị trí \(k\) sau \(n\) bước, ký hiệu là \(P(S_n = k)\).
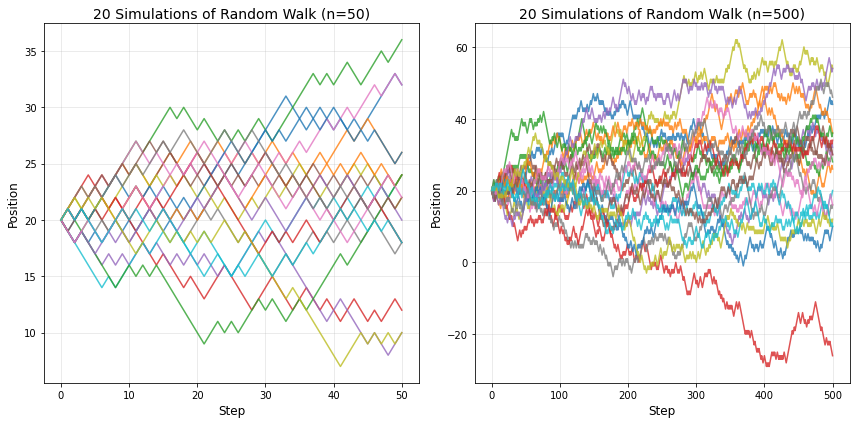
Nếu chỉ có 50 bước, biểu đồ của bạn trông sẽ rất thô và rời rạc. Nhưng nếu tăng lên 500 bước, quỹ đạo dần trờ thành những đường răng cưa liên tục. Bạn có bắt đầu thấy quen thuộc (biểu đồ giá cổ phiếu)?
2.2. Phân tích
Tại sao các nhà toán học lại dùng trò chơi này để mô phỏng thị trường tài chính? Vì Random Walk sở hữu 3 tính chất cực kỳ quan trọng sau đây:
-
Tính không có trí nhớ (Markov Property): Đồng xu không có trí nhớ. Việc hôm nay bạn tung được mặt Ngửa không làm tăng hay giảm khả năng ngày mai bạn lại tung được mặt Ngửa. Trong tài chính, điều này tương ứng với giả thuyết thị trường hiệu quả (Efficient Market Hypothesis): mọi thông tin đã phản ánh vào giá, biến động giá ngày mai là một sự ngẫu nhiên mới hoàn toàn.
-
Kỳ vọng bằng 0 (Martingale): Đây là một trò chơi công bằng, hay trò chơi có kỳ vọng bằng 0. Vì xác suất Ngửa/Sấp là \(50/50\), nên trung bình bạn sẽ không thắng cũng không thua: \(E[S_n] = S_0\). Điều này có nghĩa là: trong một thị trường ngẫu nhiên thuần túy không có xu hướng chủ đạo drift, bạn không thể kỳ vọng kiếm lời chỉ bằng cách dựa vào sự may rủi của bước đi.
-
Rủi ro tăng theo thời gian (Variance): Dù trung bình bạn đứng yên, nhưng càng tung đồng xu nhiều lần, bạn càng có khả năng đi rất xa khỏi vạch xuất phát (về cả hai phía). Sau \(n\) lần tung, độ lệch chuẩn vị trí của bạn là \(\sqrt{n}\). Rủi ro không tăng gấp đôi khi thời gian tăng gấp đôi, rủi ro tăng theo căn bậc hai của thời gian.
2.3. Lời giải
Trong thế giới ngẫu nhiên, lời giải của một bài toán không còn là một số xác định mà là tập hợp các chỉ số thống kê như phân phối xác suất (probability distribution), kỳ vọng (expectation), và phương sai (variance).
Sau đây là bảng tóm tắt lời giải cho bài toán Random Walk. Nếu không muốn đi sâu vào phần toán, bạn đọc có thể bỏ qua và tới thẳng phần Ví dụ 2.4.
| Khái niệm | Công thức | Ý nghĩa đơn giản |
|---|---|---|
| Vị trí cuối \(k\) | \(k = n_u - n_d\) | Hiệu số giữa số lần tăng và giảm. |
| Xác suất dừng tại \(k\) | \(P(S_n = k) = \binom{n}{\frac{n+k}{2}} p^{\frac{n+k}{2}} q^{\frac{n-k}{2}}\) | Tỉ lệ phần trăm ở \(k\) sau \(n\) bước. |
| Kỳ vọng | \(E[S_n] = S_0 + n(p-q)\) | Xu hướng chung của bước đi (đi lên, đi xuống hay đứng yên). |
| Phương sai | \(Var(S_n) = 4npq\) | Độ rộng của sự phân tán (đo lường rủi ro). |
2.3.1. Phân phối xác suất — “Khả năng xảy ra là gì?”
Ta có hệ phương trình dựa trên tổng số bước \((n_u + n_d)\) và vị trí cuối cùng \((n_u - n_d)\) như sau:
\[\begin{cases} n_u + n_d = n \\ n_u - n_d = k \end{cases}\]Giải hệ phương trình này, ta được:
\[n_u = \frac{n + k}{2}, \quad n_d = \frac{n - k}{2} ~~~~(4)\]Để \(k\) là một vị trí khả thi, cả \(n_u\) và \(n_d\) phải là số nguyên. Điều này có nghĩa là \(n\) và \(k\) phải cùng tính chẵn lẻ (cùng chẵn hoặc cùng lẻ) và \(\lvert k \rvert \le n\).
Xác suất để có đúng \(n_u\) bước tăng trong tổng số \(n\) bước được tính theo hệ số nhị thức:
\[\begin{align} P(S_n = k) &= \binom{n}{n_u} p^{n_u} q^{n_d} \\ &= \binom{n}{\frac{n+k}{2}} p^{\frac{n+k}{2}} q^{\frac{n-k}{2}} ~~~~(5) \end{align}\]Trường hợp đối xứng \((p = q = 1/2)\):
\[P(S_n = k) = \binom{n}{\frac{n+k}{2}} \left( \frac{1}{2} \right)^n ~~~~(6)\]Trong đó \(\binom{n}{n_u}\) là ký hiệu của tổ hợp chập \(n_u\) của \(n\) phần tử (còn gọi là hệ số nhị thức) thể hiện số cách chọn \(n_u\) phần tử từ một tập hợp gồm \(n\) phần tử mà không phân biệt thứ tự:
\[\binom{n}{n_u} = \frac{n!}{n_u!(n - n_u)!} ~~~~(7)\]Nhận xét: Phân phối xác suất (probability distribution) cho bạn biết tất cả các vùng giá có thể xảy ra sau \(n\) bước và tỉ lệ phần trăm rơi vào vùng giá đó. Điều này giúp bạn biết xác suất cổ phiếu tăng lên 100 hoặc giảm xuống 20 là bao nhiêu, với thông tin giá cổ phiếu ngày hôm nay là 80. Nếu không biết phân phối, bạn không thể biết được “vùng an toàn” của giá cổ phiếu để tránh “cháy tài khoản”.
2.3.2. Kỳ vọng — “Điểm dừng trung bình”
Tại mỗi bước, biến ngẫu nhiên \(X_i\) nhận hai kết quả: \(X_i = 1\) với xác suất \(p\) và \(X_i = -1\) với xác suất \(q = 1-p\). Kỳ vọng là trung bình trọng số của các kết quả:
\[E[X_i] = (1)p + (-1)q = p - q ~~~~(8)\]Vị trí sau \(n\) bước \(S_n\) là tổng của các bước đơn lẻ \(X_i\). Vì \(X_i\) là các biến ngẫu nhiên độc lập (bước đi hôm nay không phụ thuộc vào hôm qua) và tính chất tuyến tính của kỳ vọng, ta có:
\[\begin{align} E[S_n] &= E[S_0] + E[X_1] + E[X_2] + \dots + E[X_n] \\ &= E[S_0] + n E[S_i] \\ &= S_0 + \mathbf{n(p-q)} ~~~~(9) \end{align}\]Trường hợp đối xứng \((p = q = 1/2)\):
\[E[S_n] = S_0 ~~~~(10)\]Nhận xét: Kỳ vọng (expectation) trả lời cho câu hỏi: “Nếu bạn lặp lại mô hình này 1.000 lần, vị trí trung bình của giá cổ phiếu là ở đâu?”. Trong tài chính, điều này cũng giúp phân định tài sản tốt hay xấu. Nếu xác suất tăng \((p)\) lớn hơn xác suất giảm \((q)\), hay kỳ vọng của một bước đi ngẫu nhiên mang lại lợi nhuận dương \((E[S_n] \ge S_0)\), đó là một tài sản đáng đầu tư.
2.3.3. Phương sai — “Độ rủi ro và biến động”
Phương sai đo lường “bình phương khoảng cách” từ các kết quả đến giá trị trung bình. Công thức là:
\[Var(X_i) = E\left[ (X_i - E[X_i])^2 \right] = E\left[ X_i^2 \right] - (E\left[ X_i \right])^2 ~~~~(11)\]Tính \(E\left[ X_i^2 \right]\) dựa trên trung bình trọng số:
\[E\left[ X_i^2 \right] = (1^2 \times p) + ((-1)^2 \times q) = p + q = 1 ~~~~(12)\]Thay \((8)\) và \((12)\) vào công thức \((11)\):
\[\begin{align} Var(X_i) &= E\left[ X_i^2 \right] - (E[X_i])^2 \\ &= 1 - (p - q)^2 \\ &= 1^2 - (p - q)^2 \\ &= (p + q)^2 - (p - q)^2 \\ &= (p^2 + 2pq + q^2) - (p^2 - 2pq + q^2) \\ &= 4pq ~~~~(13) \end{align}\]Tương tự phần trước, sau \(n\) bước:
\[\begin{align} Var(S_n) &= Var(S_0) + Var(X_1) + Var(X_2) + \dots + Var(X_n) \\ &= 0 + n Var(X_i) \\ &= \mathbf{4npq} ~~~~(14) \end{align}\]Trường hợp đối xứng \((p = q = 1/2)\):
\[Var(S_n) = n ~~~~(15)\]Nhận xét: Phương sai (variance) đo lường việc giá cổ phiếu bị “văng” đi xa khỏi điểm trung bình bao nhiêu. Phương sai càng lớn, các bước đi càng hỗn loạn và khó đoán. Điều này cũng có nghĩa là cổ phiếu đó rất rủi ro; giá có thể vọt lên rất cao nhưng cũng có thể rơi xuống rất sâu. Trong tài chính, chúng ta quan tâm đến độ lệch chuẩn \((\sigma = \sqrt{Var})\) hay độ biến động (volatility) hơn là phương sai. Rủi ro không tăng tuyến tính: nếu thời gian tăng gấp 4 \((n=4)\), rủi ro chỉ tăng gấp 2 \((\sqrt{4}=2)\).
2.4. Ví dụ
Giả thiết
- Số bước: \(n = 4\)
- Xác suất tăng: \(p = 1/2\)
- Xác suất giảm: \(q = 1/2\)
- Vị trí bắt đầu: \(S_0 = 10\)
Vì mỗi bước có 2 lựa chọn (tăng hoặc giảm), với 4 bước sẽ có tổng cộng \(2^4 = 16\) lộ trình có thể xảy ra.
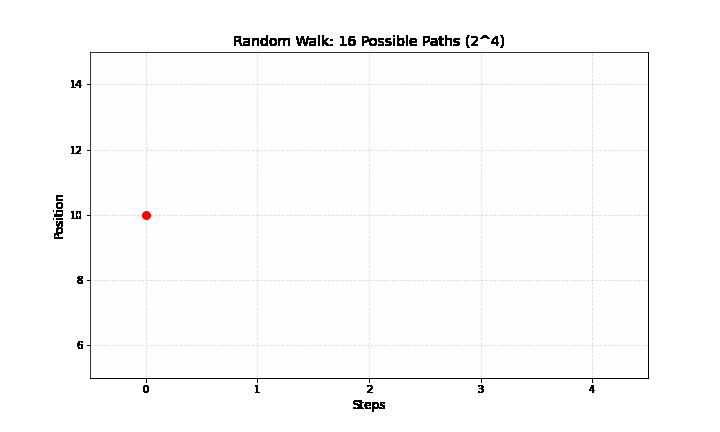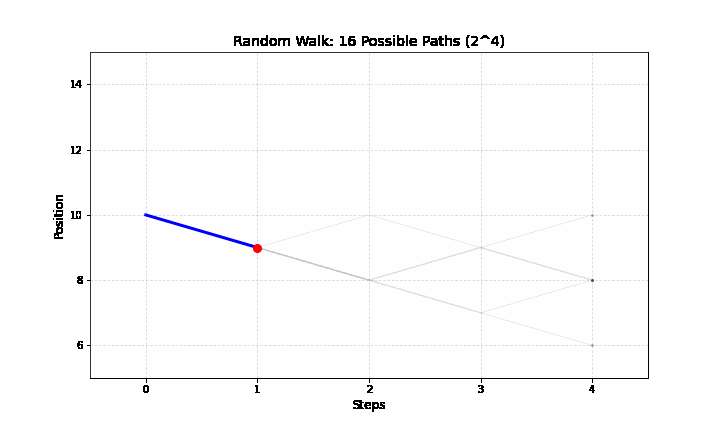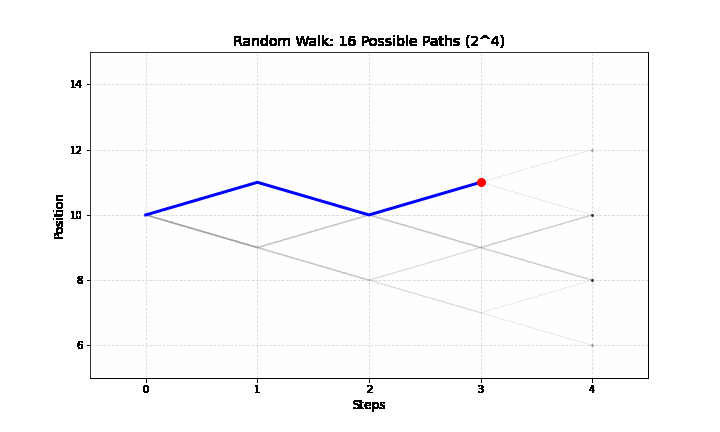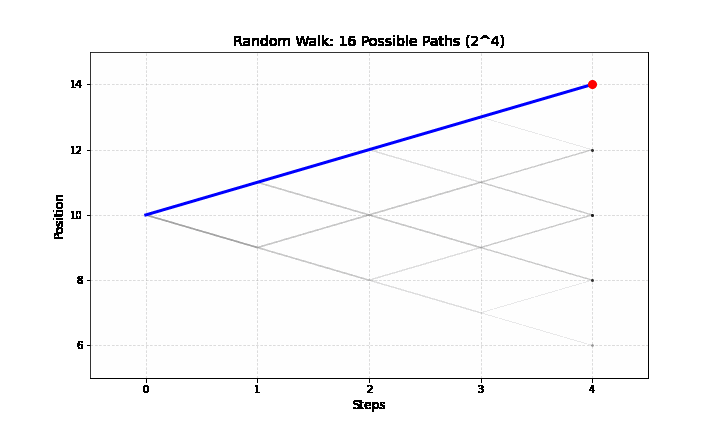
Dưới đây là bảng phân bổ xác suất cho vị trí kết thúc \(k\):
| Vị trí kết thúc \((k)\) | Số bước tăng \((n_u)\) | Số bước giảm \((n_d)\) | Cách tổ hợp \(\binom{n}{n_u}\) | Xác suất \(P(S_4 = k)\) |
|---|---|---|---|---|
| 14 | 4 | 0 | \(\binom{4}{4} = 1\) | \(1/16 = 6.25\%\) |
| 12 | 3 | 1 | \(\binom{4}{3} = 4\) | \(4/16 = 25.0\%\) |
| 10 | 2 | 2 | \(\binom{4}{2} = 6\) | \(6/16 = 37.5\%\) |
| 8 | 1 | 3 | \(\binom{4}{1} = 4\) | \(4/16 = 25.0\%\) |
| 6 | 0 | 4 | \(\binom{4}{0} = 1\) | \(1/16 = 6.25\%\) |
Xác suất cho mỗi vị trí \(k\) có thể được suy ra trực tiếp không dùng công thức tổ hợp như sau:
-
Nếu 4 bước đều tăng: Chỉ có 1 lộ trình duy nhất có thể xảy ra trong 16 lộ trình. Giá cổ phiếu tăng từ 10 lên 11, 12, 13 rồi 14 \((Tăng, Tăng, Tăng, Tăng)\). Xác suất cho lộ trình này là \(1/16\).
-
Nếu 3 bước tăng, 1 bước giảm: Có 4 lộ trình có thể xảy ra như sau: \((Tăng, Tăng, Tăng, Giảm)\); \((Tăng, Tăng, Giảm, Tăng)\); \((Tăng, Giảm, Tăng, Tăng)\); \((Giảm, Tăng, Tăng, Tăng)\). Xác suất cho những lộ trình này là \(4/16\).
Phân tích kết quả
-
Phân phối xác suất: Vì tổng số bước \(n = 4\) là số chẵn, giá cổ phiếu chỉ có thể dừng ở các vị trí chẵn \((0, \pm 2, \pm 4)\). Vị trí có khả năng cao nhất là \(k = 10\) \((37.5\%)\). Vị trí \(k = 12\) và \(k = 8\) có xác suất là hoàn toàn bằng nhau \((25\%)\).
-
Kỳ vọng: Với xác suất tăng/giảm là như nhau, kỳ vọng sẽ hội tụ về vị trí ban đầu.
- Phương sai: Các đường đi tỏa ra như một chiếc quạt. Càng về sau, khoảng cách giữa các vị trí càng lớn, minh chứng cho việc phương sai tăng dần theo thời gian.
- Độ lệch chuẩn: Mặc dù trung bình là vị trí ban đầu, nhưng thông thường giá cổ phiếu sẽ nằm cách vị trí ban đầu khoảng 2 đơn vị.
Ví dụ Python
Nếu bạn chưa cài đặt Python trên máy tính, bạn có thể sử dụng Google Colab để chạy code ngay trên trình duyệt. Tôi đã chuẩn bị source code cho ví dụ trên, bạn chỉ cần đăng nhập Gmail và nhấn vào nút bên dưới để bắt đầu.
Bạn nhấn biểu tượng hình tam giác hoặc tổ hợp phím Ctrl + Enter để chạy code. Bạn có thể thay đổi các biến để xem sự thay đổi. Đừng sợ làm hỏng nó, bạn luôn có thể tải lại trang để bắt đầu lại.
Trước tiên, chúng ta cần khai báo hai thư viện: numpy cho tính toán ma trận, đại số tuyến tính và matplotlib để vẽ biểu đồ một cách chuyên nghiệp.
import numpy as np
import matplotlib.pyplot as plt
Chúng ta khai báo các biến start_value, p, n_steps như giả thiết của bài toán. Chúng ta thêm biến n_walks cho số lần mô phỏng Random Walk, số lần càng lớn (1000 lần) xác suất thực nghiệm (empirical probability) càng chuẩn.
# Configuration
start_value = 10 # Initial position
p = 0.5 # Probability
n_steps = 4 # Number of steps
n_walks = 1000 # Number of trajectories
Tiếp theo, ta tính toán lộ trình của Random Walk.
Hàm np.full tạo ra một vector với kích cỡ \(1000 \times 1\), tất cả đều mang giá trị khởi tạo start_value. Hàm np.random.choice giúp tạo số ngẫu nhiên \((\pm 1)\) và gán vào steps — một ma trận với kích cỡ \(1000 \times 4\). Hàm np.cumsum giúp tính tổng tích lũy theo từng hàng axis=1. Nếu các bước là \([0, 1, 1, -1]\), kết quả cộng dồn sẽ là \([10, 11, 12, 11]\). Đây chính là tọa độ thực tế qua từng thời điểm.
# 1. Create starting position vector
start_pos = np.full((n_walks, 1), start_value)
# 2. Generate random steps (+1 or -1)
steps = np.random.choice([1, -1], size=(n_walks, n_steps), p=[p, 1-p])
# 3. Stack start position with steps and calculate cumulative sum
paths = np.hstack([start_pos, steps])
positions = np.cumsum(paths, axis=1)
final_positions = positions[:, -1]
Ta thử kiểm tra biến steps là “trái tim” của mô phỏng. Nếu không có sai xót gì thì ma trận này chỉ chứa hai giá trị duy nhất \((\pm 1)\). Kết quả thu được đúng như ta mong muốn!
print('steps = ')
print(steps)
steps =
[[-1 -1 -1 1]
[ 1 -1 -1 1]
[ 1 1 1 1]
...
[-1 1 -1 -1]
[-1 -1 -1 -1]
[ 1 1 -1 -1]]
Ta dùng matplotlib để vẽ biểu đồ lộ trình Random Walk cũng như biểu đồ phân phối xác suất.
# 4. Visualization
plt.figure(figsize=(12, 6))
# Subplot 1: Path trajectories
plt.subplot(1, 2, 1)
plt.plot(positions[:10].T, alpha=0.8) # plot the first 10 walks to show movement patterns
plt.title(f"Paths of the first 10 Simulations")
plt.xlabel("Step")
plt.ylabel("Position")
# Subplot 2: Final distribution (Histogram)
plt.subplot(1, 2, 2)
bins = np.arange(start_value - n_steps - 1, start_value + n_steps + 2) - 0.5 # centered on integers
plt.hist(final_positions, bins=bins, rwidth=0.8, color='skyblue', edgecolor='black')
plt.title(f"Final position distribution (n={n_steps})")
plt.xlabel("Final Position")
plt.ylabel('Number of trajectories')
plt.tight_layout() #ensure labels don't overlap
plt.show()
Biểu đồ lộ trình Random Walk được vẽ bên trái. Thuộc tính positions[:10] giúp lấy ra 10 mẫu đầu tiên trong 1000 mô phỏng để tránh làm rối biểu đồ. Biểu đồ phân phối xác suất (Histogram) được vẽ bên phải nhờ hàm plt.hist.
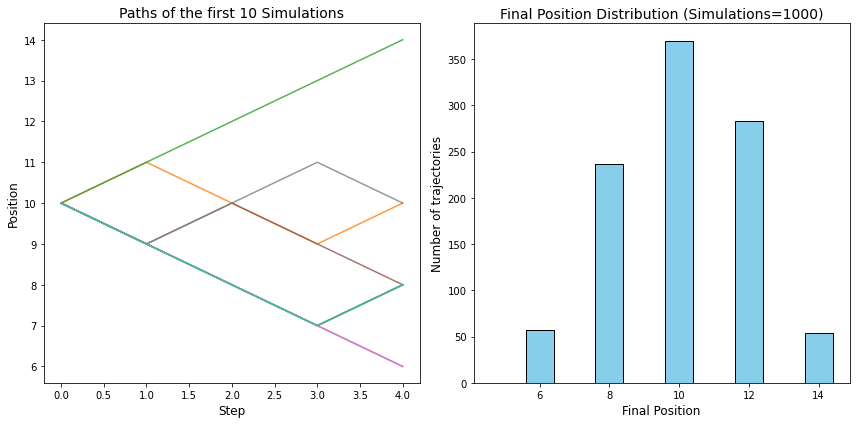
Hai cột 8 và 12 trong biểu đồ Histogram có vẻ không bằng nhau (cột 8 thấp hơn cột 12). Ta thử tính lại *xác suất thực nghiệm (empirical probability) xem sao. Hàm np.unique giúp đếm xem có bao nhiêu vị trí cuối là duy nhất và ở mỗi vị trí này có bao nhiêu mẫu.
# 5. Calculate probabilities
# Find unique value and count their occurrences
unique_values, counts = np.unique(final_positions, return_counts=True)
probabilities = counts / n_walks
print("--- Empirical Probability: ---")
for val, prob in zip(unique_values, probabilities):
current_count = counts[np.where(unique_values == val)[0][0]]
print(f"Position {int(val):>2}: {prob:>6.2%} (Count: {int(current_count)})")
--- Empirical Probability: ---
Position 6: 5.70% (Count: 57)
Position 8: 23.60% (Count: 236)
Position 10: 37.00% (Count: 370)
Position 12: 28.30% (Count: 283)
Position 14: 5.40% (Count: 54)
Kết quả thực nghiệm hơi lệch so với kết quả lý thuyết ta tính được trong bảng 2. Xác suất thực nghiệm tại vị trí 8 là \(23.60\%\) thấp hơn khá nhiều so với vị trí 12 là \(28.30\%\), và khác với tính toán lý thuyết \(25.0\%\). Điều này có thể lý giải bởi số lần mô phỏng vẫn chưa đủ lớn (1000 lần).
Ta thử thực hiện lại với số lượng bước đi nhiều hơn n_steps (500 bước) và tăng số lần mô phỏng n_walks (100 000 lần).
n_steps = 500 # Number of steps
n_walks = 100000 # Number of trajectories
Hàm plt.hist cần được sửa lại bằng cách tăng số lượng cột bins=50 và gán density=True giúp đổi trục tung từ “số lượng” thành “mật độ xác suất” (tổng diện tích các cột bằng 1).
# Increase the number of bins to show more detail (more columns)
# density=True changes the y-axis from 'Count' to 'Probability Density'
plt.hist(final_positions, bins=50, color='skyblue', edgecolor='black', alpha=0.7, density=True,
label='Simulated Results')
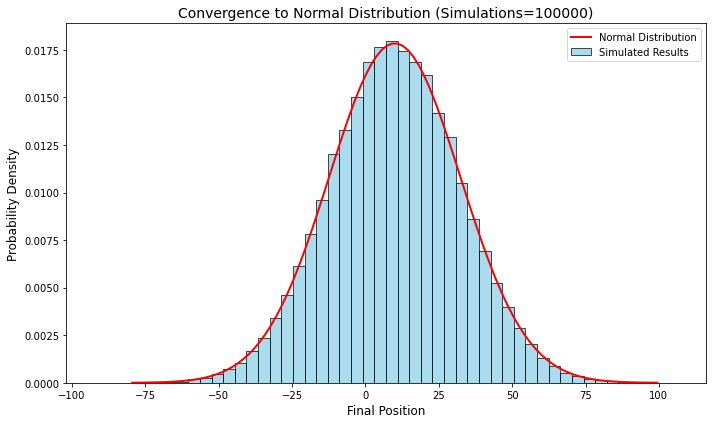
Khi tăng nhanh số bước đi n_steps và số lần mô phỏng n_walks, Histogram sẽ không còn là các cột tách rời như trong phân phối nhị thức (Binomial Distribution) mà dần hội tụ về một đường cong hình chuông mượt mà của phân phối chuẩn (Normal Distribution).
Với số bước n_steps tăng từ 4 lên 500, bạn sẽ thấy “độ rộng” của các vị trí cuối cùng dãn ra rất nhiều. Điều này chứng minh về mặt toán học rằng sự không chắc chắn (rủi ro) sẽ tăng lên theo thời gian.
Ví dụ Excel/VBA
Bạn có thể download file Excel bên dưới để bắt đầu thực hành.
Worksheet 1 “Standalone Random Walk”: Trang tính này mô phỏng quỹ đạo của một Random Walk đơn lẻ, giúp bạn hình dung cách một chuỗi các bước độc lập tiến triển theo thời gian. Bạn có thể điều chỉnh các tham số để quan sát các hành vi ngẫu nhiên khác nhau.
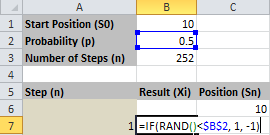
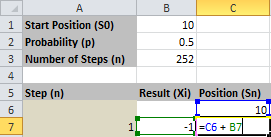
Công thức tại ô B7 như sau.
=IF(RAND() < $B$2, 1, -1)
Hàm RAND() được dùng để tạo một số ngẫu nhiên bất kỳ từ 0 đến 1. Xác suất \(p\) ở $B$2 như “vạch kẻ đường”: nếu số ngẫu nhiên nhỏ hơn \(p\) ta coi như một bước tiến \((+1)\), và ngược lại là một bước lùi \((-1)\). Như vậy chúng ta đã tạo ra được một bộ sinh số ngẫu nhiên với hai giá trị duy nhất \(\pm 1\).
Công thức tại ô C7 như sau.
=C6 + B7
C6 là vị trí quá khứ, B7 là biến động của hiện tại. Vị trí hiện tại là tổng của vị trí trước đó và biến động hiện tại. Dựa trên kết quả từ C6:C258, ta vẽ được biểu đồ lộ trình Random Walk như dưới đây.
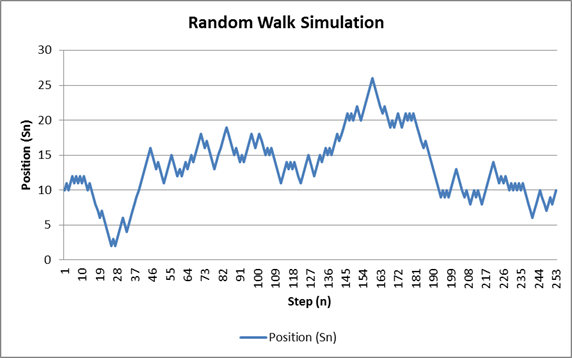
Bạn có thể nhấn phím F9 trong Excel để hàm RAND() sinh một bộ số ngẫu nhiên mới. Bạn sẽ thấy lộ trình Random Walk lúc thì vọt lên cao, lúc thì tụt sâu xuống dưới, dù thông số \(p=0.5\) không đổi.
Bạn cũng có thể thử đổi giá trị ô B2 thành \(p=0.65\) (xu hướng tăng nhẹ), bạn sẽ thấy biểu đồ bắt đầu có xu hướng dốc lên rõ rệt.
Worksheet 2 “Distribution Analysis”: Trang tính này minh họa cho ví dụ Random Walk 4 bước ở trên. Nó bao gồm biểu đồ Histogram so sánh tần suất quan sát thực nghiệm với phân phối nhị thức lý thuyết.
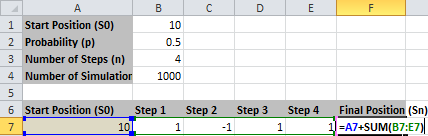
Công thức tại ô F7 như sau.
=A7 + SUM(B7:E7)
Đây chính là công thức \((3)\), vị trí hiện tại là tổng tích lũy của những “cú sốc” ngẫu nhiên trước đó và vị trí ban đầu. Khác với phần trước, kết quả F7:F1006 thể hiện vị trí kết thúc cho 1000 mô phỏng chứ không phải lộ trình cho một Random Walk duy nhất.
Công thức tại ô I7 như sau.
=COUNTIF(F:F,H7)
Ta cần đếm số lượng mẫu tại mỗi vị trí kết thúc \(6, 8, 10, 12, 14\) để vẽ biểu đồ Histogram.
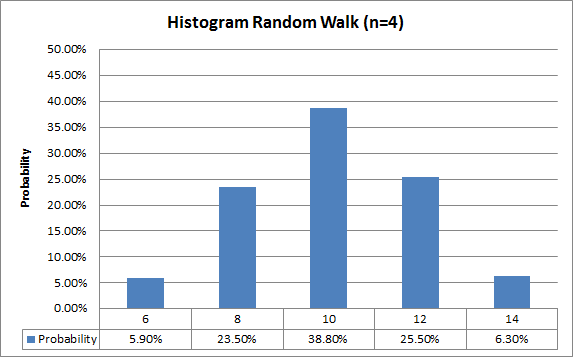
Tương tự phần Python, xác suất thực nghiệm (empirical probability) khá lệch so với tính toán lý thuyết do số lần mô phỏng chưa đủ lớn (1000 lần).
2.5. Hạn chế
Mặc dù Random Walk là nền tảng tuyệt vời, nhưng nó có những nhược điểm lớn khi áp dụng vào thực tế:
-
Tính rời rạc (Discreteness): Cổ phiếu trong thực tế được giao dịch liên tục từng giây, từng mili giây. Random Walk chỉ mô tả giá tại các mốc thời gian cố định \((t=1, 2, 3...)\).
-
Bước nhảy không đổi (Fixed Increments): Mỗi bước nhảy luôn có độ lớn cố định là \(\pm 1\). Thực tế, giá cổ phiếu có thể nhảy 1%, 3% hoặc 5% một cách ngẫu nhiên.
-
Giá trị tuyệt đối (Percentage vs. Absolute): Trong Random Walk, bước nhảy từ 10 lên 11 được coi là giống hệt bước nhảy từ 100 lên 101 (đều là \(+1\)). Tuy nhiên, nhà đầu tư quan tâm đến tỉ suất sinh lợi (%) hơn. Bước nhảy 1 trên giá 10 (10%) quan trọng hơn nhiều so với 1 trên giá 100 (1%). Điều này dẫn đến một hệ quả phi lý: giá cổ phiếu có thể rơi xuống mức âm.
Chính những hạn chế này đã thúc đẩy các nhà toán học đi tìm một phiên bản “xịn” hơn, liên tục hơn. Nếu chúng ta làm cho các bước đi ngày càng nhỏ \((\Delta t \to 0)\) và số lượng bước đi ngày càng nhiều \((n \to \infty)\) Random Walk không còn là những điểm gãy khúc rời rạc mà dần trờ thành những đường răng cưa liên tục. Đây chính là khoảnh khắc chúng ta bước vào thế giới của Black-Scholes.
3. Tóm tắt và thảo luận
Trong bài viết này, chúng ta đã có một cách nhìn mới về thị trường tài chính:
-
Từ xác định tới ngẫu nhiên: Chúng ta đã bước ra khỏi thế giới xác định (deterministic) – nơi mọi thứ đều có thể dự báo bằng phương trình vi phân kiểu Newton – để chấp nhận thế giới ngẫu nhiên (stochastic). Trong tài chính, rủi ro không phải là sai số đo lường, mà là bản chất cốt lõi.
-
Triết lý của rủi ro: Sự ngẫu nhiên không phải là sự “hỗn loạn” vô nghĩa. Như Einstein đã chứng minh qua hạt phấn hoa hay Bachelier qua giá cổ phiếu, sự ngẫu nhiên có quy luật riêng của nó và có thể mô hình hóa được thông qua xác suất.
-
Trò chơi tung đồng xu (Random Walk): Chúng ta đã mô hình hóa giá cổ phiếu một cách đơn giản nhất từ những bước đi \(\pm 1\) rời rạc. Đây là nền tảng để hiểu về các tính chất của thị trường tài chính.
Thị trường không có trí nhớ, giá ngày mai không phụ thuộc vào lộ trình ngày hôm qua.
Trong một trò chơi công bằng, kỳ vọng của bạn chính là giá trị hiện tại.
Rủi ro không tăng tuyến tính theo thời gian mà tăng tăng theo căn bậc hai của thời gian \(\sqrt{n}\).
Trước khi sang bài tiếp theo, hãy cùng suy ngẫm về một vài câu hỏi gây tranh cãi trong giới Quant:
-
Thị trường có thực sự ngẫu nhiên? Nếu giá cổ phiếu thực sự là một Random Walk, tại sao các huyền thoại như Warren Buffett lại có thể chiến thắng thị trường trong hàng thập kỷ? Liệu có một “quy luật xác định” cực kỳ phức tạp nào đó ẩn sau sự “hỗn loạn” mà chúng ta chưa thấy?
-
Rủi ro hay cơ hội? Công thức \(\sigma = \sqrt{n}\) cho thấy thời gian càng dài, rủi ro càng lớn. Nhưng trong đầu tư giá trị (mua những loại cổ phiếu có mức giá thấp hơn giá trị thực), thời gian được coi là “bạn đồng hành” giúp giảm thiểu rủi ro. Bạn đứng về phía toán học thuần túy hay thực tế đầu tư?
4. Tài liệu tham khảo
[1] Random Variables — mathsisfun.com.
[2] Random Walk Theory — investopedia.com.
[3] An Undergraduate Introduction to Financial Mathematics — J. Robert Buchanan (2006) (book).
[4] Stochastic Calculus for Finance I, The Binomial Asset Pricing Model — S.E. Shreve (2004) (book).
[5] Stochastic Calculus for Finance II: Continuous-Time Models — S.E. Shreve (2004) (book).